Merge Sort: What it is and Algorithm?

Table of Contents

Merge sort is an effective sorting algorithm based on the comparison. The algorithm is based on “Divide and conquer,” meaning the initial collection will be split into smaller pieces in this situation. Moreover, this concept can be introduced recursively so that the collection is split into single components and then rebuilt into a sorted set. The re-construction of the algorithm merging portion is the phase where the components are ordered.

In this blog post of All Assignment Help, we have explained the merge sort algorithm. The objective of this post is to give you solid baseline knowledge of the merge sort algorithm, which serves as a basis for understanding more complex algorithms.

What is Merge Sort?

Merge sort is a popular and highly effective sorting method. This particular algorithm is one you should consider if you are a software engineer getting ready for your next tech interview.

Merge sort is a general-purpose sorting algorithm that ranks lists according to comparisons between their elements. However, the majority of algorithms that use this sorting provide stable sorts, meaning that the order of any two equal entries in the sorted list and the original list does not change.

Merge sort operates consistently and quickly for a given amount of data. As such, it is not recommended for sorting an array that is nearly sorted. Sorting linked lists is a good use for it.

Read Here: Bachelor of Computer Science: Best Way to Boost Your Career

Important Characteristics of Merge Sort

Let’s explore some of the important characteristics of merge sort:

In order to sort linked lists, Merge Sort is helpful.
Merge Sort is a stable sort, meaning that the same component in an array maintains its initial positions in relation to each other.
Merge sort overall time complexity is O(nLogn). It is more efficient because the runtime is also O(nlogn).
In the worst case, the space complexity of the Merge sort is O(n). This implies that for the last information sets this algorithm requires a lot of room and can slow down activities.

Merge sort is comparable to the rapid sort algorithm as it sorts the components using a divide-and-conquer strategy. Additionally, the sorting method in question is highly effective and widely used. The provided list is split in half equally, it calls for the two halves, and it then combines the two sorted parts.

The Process of Merge Sort

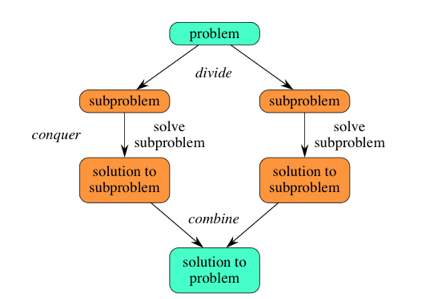
The process involves three parts:

Dividing the issue into a number of smaller subproblems of the same issue.
Conquering the subproblems by continuously solving them. Solve the subproblems as basic cases if they are small enough.
Combine the subproblem alternatives into the initial issue solution.

Implementing Merge Sort

The function of merge sort should sort the subarray array [p. r] recursively. It means after calling sort on (array, p, r), the components should be sorted in ascending order from index p to index r of the array.

The algorithm of merge sort explains that: –

It is essential to realize that sorting needs to be performed if the size of the sub-array is 0 and 1. Therefore, nothing needs to be done.
Otherwise, to sort the subarray, the merge type utilizes divide-and-conquer.
To combine the sorted sub-arrays array [p. q] and array [q+1.. r], use merge (array, p, q, r).

Uncomment the Program.assertEqual function at the bottom once implemented to verify the passing of the test assertion. However, it is not easy to understand the implementation of merge sort in one go. You should consult an online computer programming assignment help expert who will not only help you understand the process involved in merge sort implementation but also assist you in completing your assignments.

What Is the Process of the Merge Sort Algorithm?

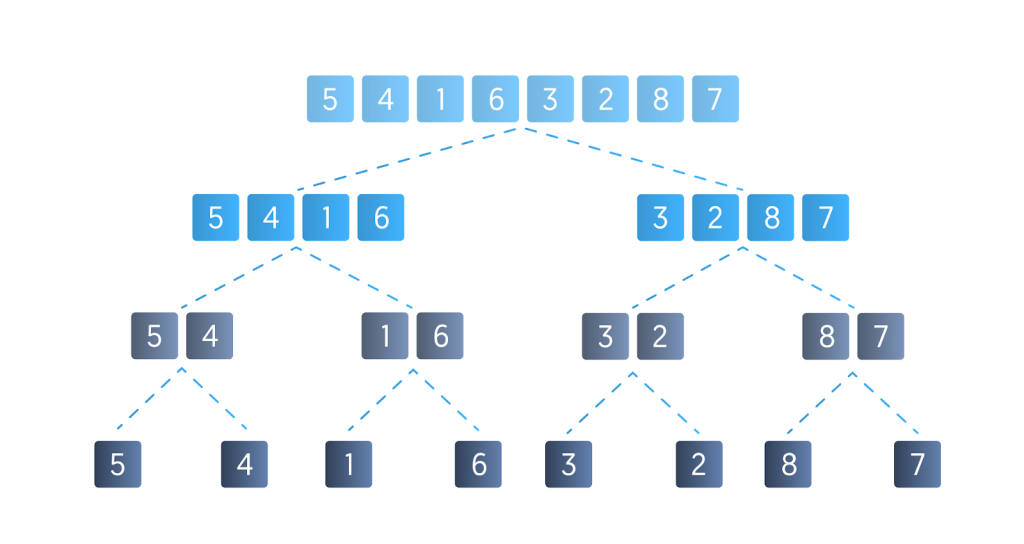
Step 1: Separating the List into Two More Compact Sublists

The list is divided into smaller sublists, and the sublists are sorted using a recursive call. Furthermore, the sublists are then subdivided into smaller sublists by the recursive call used in the sorting process.

This process keeps going until the list’s size drops to just one.

Step 2: Create the Sorted List by Combining the Sublists

As of right now, our sublists are already arranged. We just need to combine them at this point.

The lists are merged from top to bottom. The lists in the bottom row of the above picture are all of size 1, as can be seen above in the image. However, these lists can be categorized as “sorted” as they only have one element.

We will combine the previously sorted 1-element lists in order to sort the lists in the second row from the bottom. Sorted lists of size 1 are first combined to form sorted lists of size 2, which are then combined to make sorted lists of size 4, and so forth.

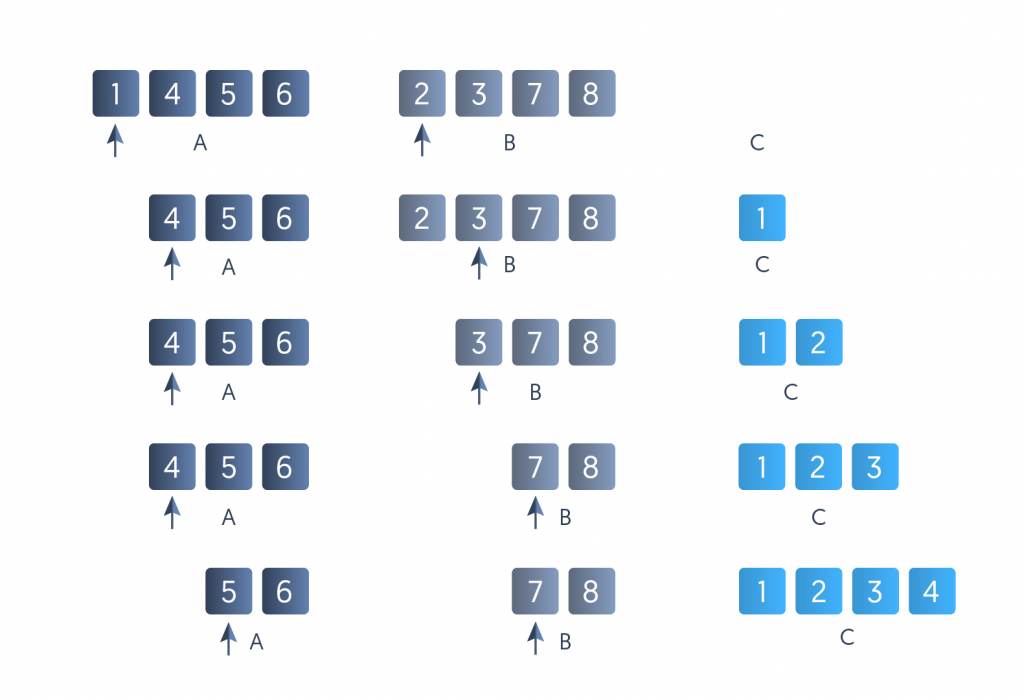
The process of merging will continue until we have a single list of size n.

The process of merging the sort algorithm is intricate. However, if you make a proper lesson plan assignment, you can conquer this process easily. This will also help you avoid making mistakes during the execution of the algorithm process.

Also Read: Computer Science Engineering: A field of high opportunity

Pseudocode for Merge Sort

Now that we understand the operation of merge sort, let’s write some pseudocode. This allows you to write code in any programming language that you choose.

Declare two variables, left and right, to indicate the array’s extreme indices.
The numbers on the left and right will be 0 and n-1, respectively.
Determine mid = (left + right)/2.
Call merge Sort on the left, middle, and rear (mid+1).
The above will go on until left and right.
After that, we will call merge for the two subproblems.

Complexity of Merge Sorts

Time Complexity

It is essential to comprehend Merge Sort’s time complexity since it sheds light on the effectiveness of the algorithm. The term “time complexity” basically describes the computational complexity that assesses how long an algorithm takes to execute, with the size of the input being a contributing component.

Analyzing algorithms in computer science requires an understanding of time complexity. However, the time it takes for an algorithm to run in relation to the amount of input data is measured by its temporal complexity. It is represented by Big O notation. Additionally, it reflects the maximum time complexity in the worst-case situation.

Space Complexity

The space complexity of the merge sort is represented by O(n).

Space complexity considers exclusively the auxiliary space in which the problem is solved. Here, it makes no difference how much space was used to store the input data. Auxiliary space was only used to create a temporary array that held the combined lists’ outcome. The total of the sizes of the lists that are being merged is the amount of space needed.

However, in the worst situation, this might equal n. Thus, O(n) is the space complexity.

There is a lot to study under merge sort. You cannot learn about of all them by reading books and watching tutorial videos. The best way to learn merge sorts from the inside out is to take an online course. In an online course, you will get to know everything easily there is you need to know about merge sorts and their algorithms. Also, there are a range of online class help services available whom you can ask, please take my online class for me to get the most out of your online course.

Examples of the Merge Sort Program in Java

Merge sort is the sorting technique that follows the approach of dividing and then conquering. For instance, think of an Array called A having n number of elements in it. The algorithm of this sorting theme would be processing the elements in the following 3 steps.

If it is found out that the array A contains 0 or only 1 element, then it is already said to be sorted in the given order. If it is not sorted then it would divide the array into two sub-arrays of equal parts.
The conquering part involves sorting the two arrays made in the previous step with the help of merge sort.
Finally, all the sub-arrays are merged into a single and final file which is sorted in the given manner thereby maintaining the order of the given array elements.

Algorithm:

The process merge sort program in Java programming requires you to keep a keen eye on the whole algorithm process. However, if you find yourself struggling at any point and miss any step or code in between, you can always turn to Java assignment help online. The Java programming experts hold vast knowledge and will help you at every stage with your merge sort program in Java.

FAQs

Is the sorting algorithm used by merge sort stable?
A sorting method is considered stable when there is no change in the order of any two equal elements between the original and sorted lists. The way we use the algorithm will determine this. This algorithm produces a stable sort in the majority of implementations.

Does merge sort use an algorithm for in-place sorting?
An in-place algorithm uses no additional memory space to analyze the input and generate the result in the same location as the input. However, merge sort is not an in-place sorting method because we use an auxiliary array to store the combined list momentarily.

What does a two-way merge sort in a data structure mean?
It is the initial item in each list is compared by the 2-way merging process, which then places the smallest item at the head of the output list.

What two purposes does merge sort carry out?
The two main purposes of merge sort are splitting and merging. An unsorted list is initially divided into smaller sublists until each one is made up of a single element. It then combines and sorts these smaller lists into a single, sorted list by merging them in a sorted order. This process is repeated until the entire list is sorted.